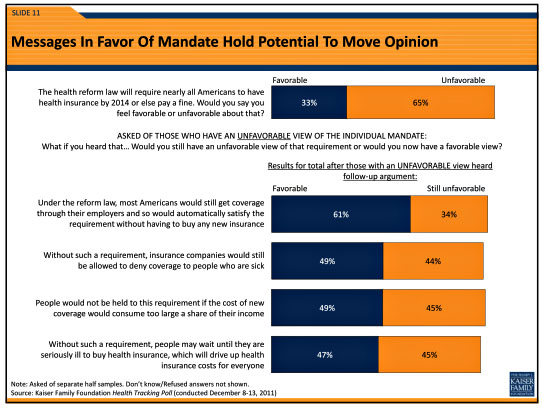
Sarah Kliff points us today to yet another Kaiser poll on Obamacare, which yet again finds that people hate the individual mandate. However, the Kaiser folks also find that some arguments in favor of the mandate reduce the level of opposition:
This got me thinking. I just finished reading Daniel Kahneman’s Thinking, Fast and Slow, which naturally got me thinking about Prospect Theory, one of my favorite socio-econo-behavioral theories of the past few decades. There’s a lot to Prospect Theory, but its most famous aspect is its focus on loss aversion. Most people, it turns out, aren’t so much risk averse as they are loss averse: they prefer a sure gain over a gamble for a bigger gain, but they prefer a gamble when the alternative is a sure loss. Bottom line, people really, really hate to lose things that they already have.
This sounds obvious, but it turns out to have a lot of useful and nonobvious applications. And now, I’m wondering how it could apply to the mandate. In its usual form, the individual mandate forces people to take a guaranteed loss. Basically, this is the question people are being asked:
Would you rather take a sure loss now (i.e., be forced to pay for health insurance) or take a gamble that you’ll be healthy for the next year and won’t have to pay anything?
Put that way, people tend to be loss averse and they dislike the mandate. So here’s the question: is there a way this can be reframed into a sure gain vs. a gamble for a bigger gain? If it can, then most people will prefer the sure gain. However, I’m not very creative and I can’t really think of anything. It would probably be something along these lines:
Almost everyone gets sick eventually. Would you rather be guaranteed proper treatment when you get sick, or take a gamble that you’ll never get sick and you’ll come out ahead on health insurance premiums?
That’s not very convincing. But maybe the hive mind can think of something better. There’s not really much going on for the rest of this week, so this is as good a question to ponder as anything.